日本弁理士会の活動

ACTIVITY

  • SHARE
  • Facebook
  • Twitter
  • はてなブックマーク
  • LINE

先生のための（知財の）ひきだし！数学編

大人でも思わず引き込まれるおもしろ知財エピソード集です。 小学生から高校生までを対象に幅広くご利用ください。

テーマ：コンパスの補助具

Keywords コンパス、補助具、実用新案
法域 特許法、実用新案法
教科 数学、算数

コンパスは、円を描くときなどに使う２本足の道具で、足先についた針を中心に回し、もう片方の先につけた鉛筆で円を描きます。小学校３年生の算数で使い方を勉強します。
小学校３年生の男子児童が、３年生になって５月に初めてコンパスを使った際、１つの円を描くのに１時間もかかってショックを受けました。片手で持つと針が紙から外れてしまうし、指で一気に回すこともできませんでした。
そこで、そのコンパスを簡単に使うことができる「補助ハンドルつきラクラクコンパス」を発明（考案）し、第76回全日本学生児童発明くふう展で上位の「入選」に選ばれ、実用新案登録されました。（実用新案登録第３２１５５５７号）
仕組みはシンプルで、ペットボトルのキャップの中央に穴を開け、コンパスの細い持ち手にかぶせ、その上に鉛筆けずり器から取ったハンドルをつけました。ペットボトルのキャップの部分を片手でしっかり持って支え、反対の手でハンドルを回すと、うまく円を描くことができます。「おさえて回す」というコンパスのコツが身につくようになっています。



１　　コンパス用補助具
２　　ハンドル
２１　装着部
２３　ハンドルつまみ
３　　把持部
６　　コンパス

 

※ 　図は実用新案登録公報より引用したものです


（履歴情報）2020/09/14　掲載

テーマ：フラクタル日除け

Keywords フラクタル構造、シェルピンスキーのガスケット、幾何学
法域 特許法、意匠法
教科 数学

　自然界には、一見すると複雑でランダムに見えて、規則性が隠れていることがあります。そのような規則性として、例えば、海岸線、雲の形や人体の血管の枝分かれ構造などに現れるフラクタルが有名です。
　そんな、自然の中で見出される数学的な神秘に着想を得た、「フラクタル日除け」という発明があります。先に行われた東京２０２０オリンピック・パラリンピックにおいても暑さ対策として使われました。
　フラクタルとは、図形の部分を拡大すると元の図形が現れる性質、自己相似性を有することを特徴とした構造をいいます。例えば、下図にあるシェルピンスキーのガスケットは、正三角形から各辺の中点を結んでできた三角形を切り取るという操作を延々と繰り返すことで作成することができます。



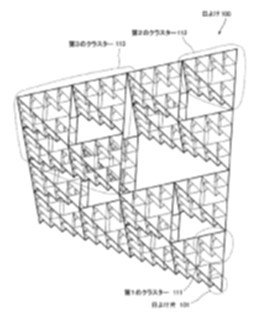　森の樹木の葉の分布は、シェルピンスキーのガスケットを四面体に拡張したシェルピンスキー四面体というフラクタル構造を有すると言われています。
　このシェルピンスキー四面体の形に小さな葉っぱを模した小片を並べて、人工的に木陰を作る発明について特許権が与えられています（特許5315514（※１）：左図）。
　この発明は、「多数の小さな葉が一定の空間中にフラクタル構造をなすように分布するという植物の構造が、太陽光を遮りつつ、太陽光に由来する熱を効率よく大気へと放出するのに適しているのではないかとの着想」を得て生まれたそうです。　　　　　　　　　　　　　　　　　　　　　　　
　上記のような「図形」は、数学の分野である幾何学の対象となるものですが、特許権による保護の対象となる発明は、”自然法則”を”利用したもの”である必要があり、実は、数学上の公式それ自体は、発明に該当すると言えず、特許を受けることができません。一方で、今回紹介した「フラクタル日除け」のように、自然法則を利用したアイディアとして落とし込むことにより、特許を取得することができる場合があります。また、特許のほか、物品の形状について、美観の観点から意匠登録受けることができる場合もあります（例えば、意匠登録1398775）。

（※１） https://www.j-platpat.inpit.go.jp/c1800/PU/JP-5315514/199076F1B5CE24A28C94C05968EC44CBD6DF69DA0239BA24E76AF94C69AC773A/15/ja

（履歴情報）2023/03/23　掲載